Test分类

Solidity 测试/审计

原文：https://github.com/Cyfrin/sc-exploits-minimized/blob/main/src/invariant-break/README.md

Invariant（不变量）

不变量是程序或系统的属性，必须始终保持真实。

所有系统都至少具有一种不变性。甚至 ERC20/ERC721 代币也有不变性，Trail of Bits Properties repo中有一些不变性的例子。

考虑到这点，我们理解了系统的不变量，我们就可以编写测试来专门测试这些不变量

测试不变量的四个等级

关于不变量的研究，大致可分为如下四个等级：

• Stateless fuzzing（无状态模糊测试）
• Open Statuful fuzzing （开放有状态模糊测试）
• Handler Stateful fuzzing （基于处理程序的有状态模糊测试）
• Formal Verification（形式化验证）

1. Stateless fuzzing - Open

无状态模糊测试（一般称为“模糊测试（fuzzing））是指向函数提供随机数据以破坏某些不变量或属性

它是无状态的，因为在每次模糊测试运行后，他都会重置状态，或者重新开始

示例

我们可以把它想象成测试什么方法打破气球。

1. Fuzz run 1:
   1. 得到一个新的气球
      1. 做一件事来尝试打破它（即：打它、踢它、放下它）
      2. 记录它是否被打破
2. Fuzz run 2:
   1. 得到一个新的气球
      1. 做一件事来尝试打破它（即：打它、踢它、放下它）
      2. 记录它是否被打破
3. Repeat…

优点 & 缺点

• 优点：
  • 书写迅速
  • 测试迅速
• 缺点：
  • 它是无状态的，因此通过调用不同的函数来破坏属性，不会发现问题
  • 你永远不能 100% 确认它有效，因为它是随机输入

2. Stateful fuzzing - Open

有状态模糊测试是当你想系统提供随机数据时，新的测试是从上一次的模糊测试的结束状态开始进行测试。

更简单的说，就是像同一个合约输入随机数据

示例

我们可以把它想象成测试什么方法打破气球。

1. Fuzz run 1:
   1. 得到一个新的气球
      1. 做一件事来尝试打破它（即：打它、踢它、放下它）
      2. 记录它是否被打破
   2. 如果没破
      1. 尝试用不同的方式弹出它（即：拳打脚踢，放下）
      2. 记录它是否被打破
   3. 如果没有打破…重复一定次数
2. Fuzz run 2:
   1. 得到一个新的气球
      1. 做一件事来尝试打破它（即：打它、踢它、放下它）
      2. 记录它是否被打破
   2. 如果没破
      1. 尝试用不同的方式弹出它（即：拳打脚踢，放下）
      2. 记录它是否被打破
   3. 如果没有打破…重复一定次数
3. Repeat

在这里我们可以看到区别，我们没有在每次“模糊运行”中都得到一个新气球。在有状态模糊测试中，我们继续在对之前同一个气球尝试了许多事情。

优点 & 缺点

• 优点：
  • 书写迅速（没有 stateless fuzzing 快）
  • 可以查找来自特定顺序调用函数的 bug
• 缺点：
  • 我们可能遇到”路径爆炸”，其中可能的路径太多，而模糊器什么也没找到
  • 你永远不能 100% 确认它有效，因为它是随机输入

3. Stateful Fuzzing - Handler

基于处理程序的有状态模糊测试与开放状态模糊测试相同，只是我们限制了我们可以执行的”随机”操作的数量

如果我们有太多的选择，我们可能永远不会随机到一些真正会打破我们不变性的东西。因此，我们将随机输入限制为一组可以调用的特定随机操作

示例

我们可以把它想象成测试什么方法打破气球。

1. Fuzz run 1:
   1. 得到一个新的气球
      1. 做 1 件事来尝试弹出它（放下它或踢它）
      2. 记录它是否被打破
   2. 如果没破
      1. 尝试用不同的东西来弹出它（放下它或踢它）
      2. 记录它是否被打破
   3. 如果没有打破…重复一定次数
2. Fuzz run 2:
   1. 得到一个新的气球
      1. 做 1 件事来尝试弹出它（放下它或踢它）
      2. 记录它是否被打破
   2. 如果没破
      1. 尝试用不同的东西来弹出它（放下它或踢它）
      2. 记录它是否被打破
   3. 如果没有打破…重复一定次数
3. Repeat

这需要在 Foundry 中设置更多的工作，在这里可以看到例子：

优点 & 缺点

• 优点：

  • 可以查找来自按特定顺序调用函数的 bug。
  • 限制了可能路径太多的“路径爆炸”问题，因此模糊器更有可能发现问题

• 缺点：

  • 正确书写要长得多
  • 限制太多来进行测试会容易，但是这样你就会错过潜在的错误

Handler fuzzing 和 Open fuzzing 的区别

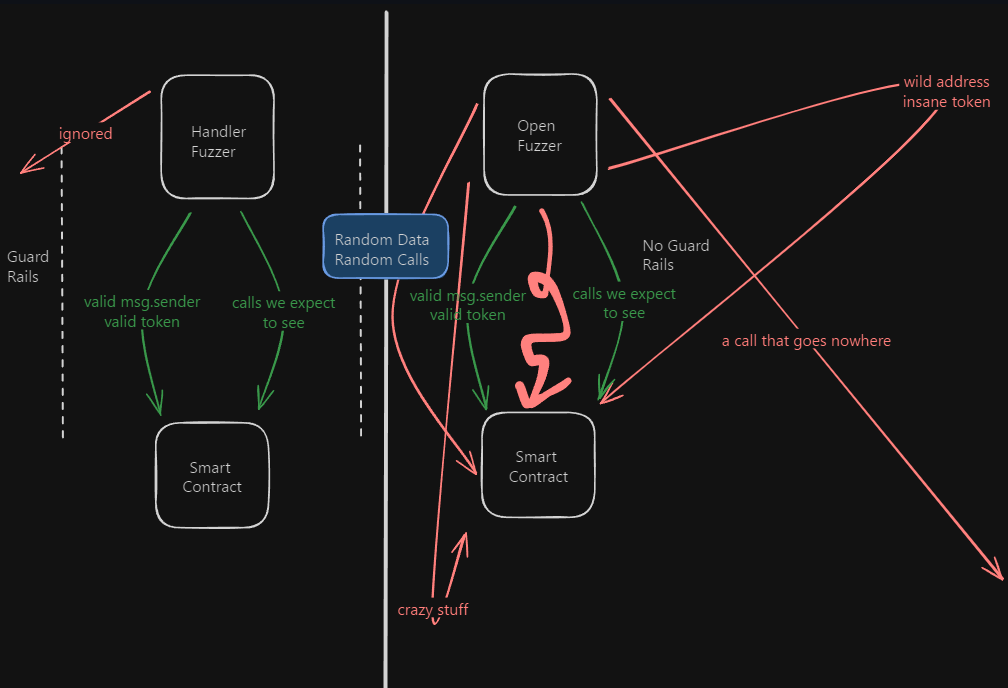
4. Formal Verification

形式验证是在数学上证明程序做特定事情或证明它不做特定事情的过程。

对于不变量，证明我们的程序总是发挥我们的不变量会很好。

进行形式验证的最流行方法之一是通过符号执行。符号执行是一种分析程序的方法，以确定哪些输入导致程序的每个部分执行。它会将程序转换为符号表达式（因此得名）来解决这个问题。

FV TL;DR

总结来说，FV 是：

他将你的函数转换为数学，然后试图证明这些公式的属性。数学是可证明的 。数学是可以被解出来的，函数不能（除非将他们转化为数学）。

Example

举例，对以下的函数进行：

function f(uint256 y) public {
	uint256 z = y * 2;
	if (z==12) {
	revert();
	}
}

如果我们想要去证明函数 f 有一个输入，使它永远不会回滚，我们将其转换为数学表达式，如下所示：

z == 12 && // is z == 12, the program reverts
y >= 0 && y < type(uint256).max && // y is uint256, so it must be within the uint256 type
z >= 0 && z < type(uint256).max && // z is also a uint256
z == y * 2 // our math

上述语言被称为 SMTLIB，一种用于符号执行的领域特定语言

在这个示例中，我们有一组 4 个布尔表达式。

SAT Solver （SAT 求解器）

然后，我们将这组逻辑表达式转储到 SAT求解器（SAT Solver SAT 求解器不是符号执行，但这是现在很流行的下一个步骤）。现在，我们把它想象成一个黑盒，采用布尔表达式，并试图找到一个”满足”集合的例子，对于上面的示例，我们寻找一个输入 y，使得其余布尔值为 true。

要将其转储到 SAT 求解器中，我们需要将数学转换为 CNF 形式，看起来类似于这样：

(z <= 12 OR y < 0 OR z < 0) AND (z >= 12 OR y < 0 OR z < 0) AND (z <= 12 OR y < 0 OR z > 2y) AND (z >= 12 OR y < 0 OR z > 2y) AND (z <= 12 OR y >= 0 OR z < 0) AND (z >= 12 OR y >= 0 OR z < 0) AND (z <= 12 OR y >= 0 OR z > 2y) AND (z >= 12 OR y >= 0 OR z > 2y)

然后，我们的 SAT 求解器将尝试在我们的布尔值集中找到一个矛盾，方法是将布尔值随机设置为 true/false，并查看等式的其余部分是否成立。

他与模糊器不同，因为模糊器会尝试y的输入，而 SAT 求解器将尝试不同的布尔值输入。

优点 & 缺点

• 优点
  • 可以 100% 确定属性为 true/false
• 缺点
  • 可能很难去开始
  • 在很多情况下都不起作用（例如路径太多）
  • 工具运行速度可能很慢
  • 可以给你一种没有错误的虚假安全感。FV 只能针对一个特定属性进行保护

资源

• ToB properties:基于 ERC20、ERC721、ERC4626 和其他代币标准的属性进行模糊测试。
• Example list of properties
  属性列表示例
• Invariant/Stateful fuzz tests
  不变/有状态模糊测试
• Handler based testing using WETH
  使用 WETH 进行基于处理程序的测试