Q1ngying

今朝梦醒与君别，遥盼春风寄相思

0%

流密码

发表于 更新于 分类于 ，
本文字数： 5.1k 阅读时长 ≈ 17 分钟

根据德国 Christof Paar 的密码学基础教程学习了一些入门的密码学知识，本文对应其第二、三节内容，主要关于流密码，随机数生成器（RNG），一次性便签簿，线性同余生成器（LCG），线性反馈移位寄存器（LFSRs）以及针对LCG和LFSRs的攻击。

流密码（Stream Ciphers）简介

密码学（cryptography）可以分为三个分支：

  • symm cryptography 对称密码学
    • stream cryptography 流密码
    • block cryptography 分组密码
  • asymm cryptography 非对称密码学
  • protocols cryptography 协议密码学

motivation（动机）

在我们传播一些信息时（如手机信号）我们需要对其进行加密：

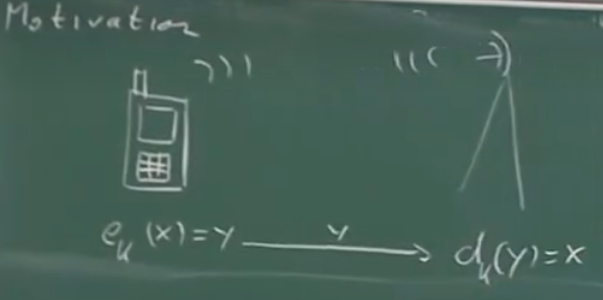
image-20240311204616816

这个$\bigoplus$表示 模2 计算

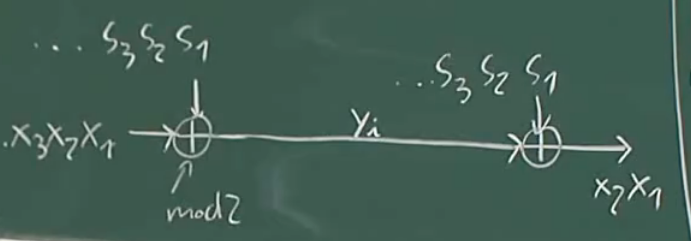
image-20240311210545513

上述就是流密码的加密过程。

定义

什么是流密码？流密码对各个位进行单独加密

在流密码中，我们用 si 来代表密钥，而不是使用 k 。
$$
encrypts:\ y_i=e(x_i) \equiv x_i+s_i \ mod \ 2 \
decrypts:\ x_i=d(y_i) \equiv y_i+s_i \ mod \ 2
$$

问题一：为什么加密，解密都是使用的相同的运算符

$$
d(y_i) \equiv y_i+s_i \ mod \ 2 \
\equiv (x_i+s_i)+s_i \ mod \ 2 \
\equiv x_i+2 \ s_i \ mod \ 2 \ \ \ \ \ \ \ \ \
\equiv xi
$$

上面的推导过程能够得到：mod 2 加法和减法是相同的运算

所以，加密和解密使用的相同的运算符
$$
x_i,y_i,s_i \in Z_2 = {0,1}
$$
上述三者在 2 的整数环中（比特 bits）

仔细观看 mod 2 情况下的相加：

xi si yi
0 0 0
0 1 1
1 0 1
1 1 0

从上面的真值表可以看出，在电气工程中，这个是异或门，所以mod2 与 异或（XOR）是相同的

继续观察，我们可以发现，当key=0时，明文的值没有变化，key=1时，明文的值发生了翻转

举例：ASCII加密”A”

$$
x_1 \ldots x_7=1000001 \
S_1 \ldots s_7 = 0101101 \
y_1 \ldots y_7 = 1101100\
$$

1101100对应的ASCII码时 l 也就是说，加密后的明文A在传输过程中被截获获取到的就变成了l。接下来对密文进行解密：
$$
1101100 \
0101101 \
1000001
$$
得到原来的明文A

流密码看起来加密解密过程很简单，但是对实际生活确实产生了很大的帮助和影响，其实最难的是下面的问题

问题：我们如何产生密钥Si的比特流？

某种程度上与随机性有关

随机数生成器（Random Number Generators:RNG)

我们区分 3 种类型的 RNGs：

  • a)：真随机数生成器（True Random Number Generator：TRNG）
    • 真正的随机数源于随机物理过程，e.g. 抛硬币，彩票，噪音(热噪声)，鼠标移动，键盘输入时间间隔
  • b)：伪随机数生成器（Pseudo Random Number Generators：PRNG）
    • RNGs是计算来的，即他们是确定性的
    • 通常他们是通过下面的函数被计算出来的
    • 第一个随机数是种子值$s_0 = seed$（可能从某些地方传来，有时候这是一个真正的随机数）
    • 然后接下来的随机数是通过递归计算来的$s_{i+1}=F(s_i)$
  • c)：加密安全的伪随机数生成器（Cryptographically secure PRNGS：CPRNG）
    • CPRNG 是 PRNG 的附加属性：数字不可预测（CPRNGs are PRNGs when an additional property: the numbers unpredictable）
    • 非正式定义：给出 n 个输出位$S_1,S_{i+1}, \ldots ,S_{1+n-1}$计算上无法构建$S_{n}$

一次性便笺簿（One Time Pad）

目标：构建一个”完美”的密码

定义（完美密码）：一个密码是”无条件安全”（或信息在理论上是安全的）如果无限计算资源也无法破解

定义：

One Time Pad（OTP）是一种流密码，其中

  1. 密钥流比特来自 TRNG
  2. 每个密钥流位仅使用一次

最大缺点：密钥要和明文一样长

举例：加密一个 400M 的文件 => 8*400 MB = 3.2 Gbit 的密钥

线性同余生成器（Linear Congruential Generator：LCG ）

idea：用一个密钥流$S_i$从一个PRNG

image-20240320211248191

上图就是如今流密码加密实现足够安全的方法。（M的意思是，假设是三十位的数字，那么A，B都是30 bit 长

虽然有一个很好的随机源（seed，A，B）但是在密码学上破解这个还是很容易的：

Attack：

Oscar 知道 $X_1,X_2,X_3$（比如文件头信息或者在消息加密中，有时有某种协议头）

  • 1)：Oscar 计算$S_1,S_2,S_3$

  • 2)：计算$S_i \equiv A \cdot S_i+B \ mod \ m$（一个有两个参数的线性方程，我们需要的是两个未知数的二元一次方程组）

    $S_3 \equiv A \cdot S_2 + B \ mod \ m$

  • 当知道两个方程时，就能破解这个密码系统

解决方法：

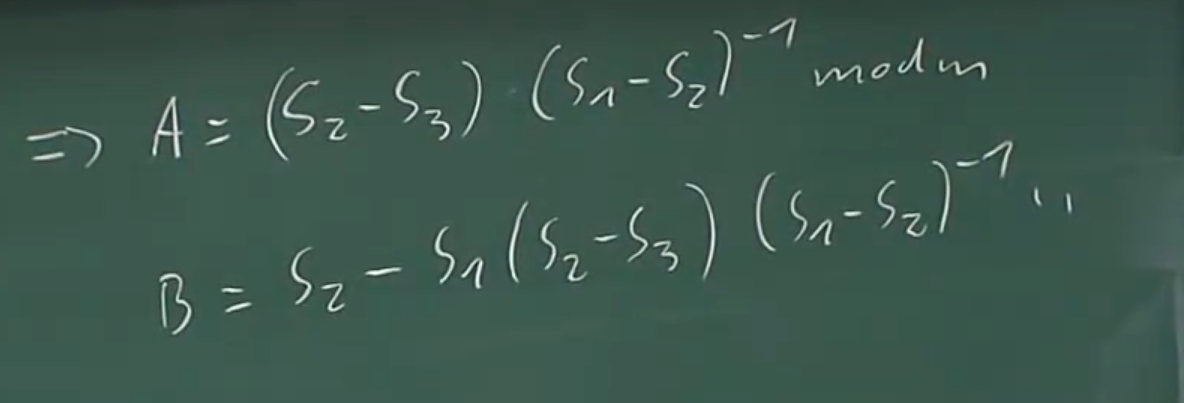
image-20240320212907748

也就是说：如果你知道三个随机数，就能破解 L

线性反馈移位寄存器(Linear Feedback Shift Registers —- LFSRs)简介

Goal：流密码在硬件加密中是较小的（低功耗）

原子元素（电器工程）：触发器(flip-flop)存储1位（1 bit）

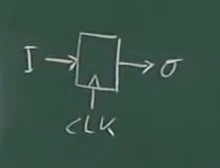
image-20240327211346820

一比特的输入，一比特的输出，然后有了时钟输入，时钟输入决定了什么时候存储比特

假设输入产生信号（下图I，但是时钟输入（clock input，下图CLK）没有输入，此时寄存器不会存储，直到时钟脉冲告诉寄存器，存储输入值（下图第一条虚线），此次存储器开始存储数据（对应的输入信号I是1，所以下图O上升），即使输入已经下降，输出元素保持不变，直到下次时钟脉冲，告诉寄存器存储输入值（这是刚好对应的输入是0），所以此时触发器的内容变成0

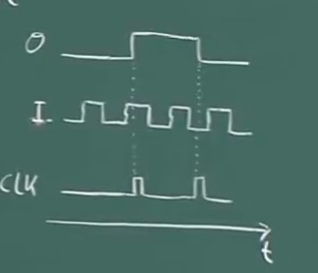
image-20240327211945817

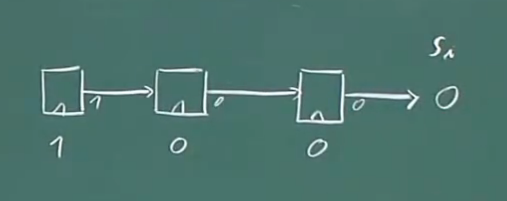
我们尝试去构建一个PRNG（通过触发器（flip-flop））：

选择三个触发器，将他们连接起来，便得到了移位寄存器，然后得到了我们的输出信号（实际上所有的系统都需要某种初始状态，必须需要大量的触发器，并为他们分配一些初始值（不能全为0））。现在我们可以看到在我们的输出得到了0

image-20240327212634402

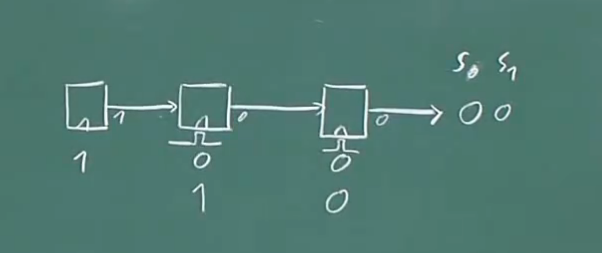
我们现在要做一些事情，否则Si保持为零。所以我们开始计时，这意味着我们产生了第一个时钟脉冲。假设我们在上图第二个触发器位置产生了一个时钟脉冲，这个触发器的输入是1，这意味着输出值变成了1，发生了右移（从最左边的触发器到中间的触发器），假设第三个触发器的位置也有一个时钟脉冲，它的输入值是0，所以他又一次把0移动存储到了第三个触发器。

image-20240327213314749

接着，第三个触发器处有一个时钟脉冲（它的输入值从0变为了1，因为第二个触发器的值在上一步变成了1），最后第三位我们得到了1。

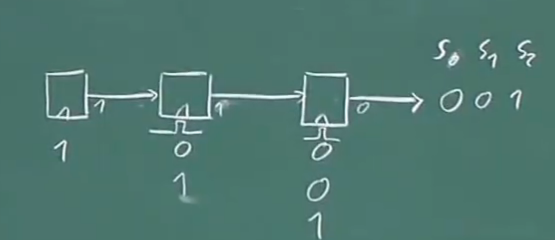
image-20240327213546517

注意，此时上面的第二个触发器发生了什么我们不知道，因为第一个寄存器的输入是空的。

所以，这是一个很愚蠢的随机数生成器，因为我们只能推出三位，我们用时钟脉冲打了三次，得到了三个输出位，game over，我们需要更聪明的随机数生成器，我们希望有一个长序列

现在到底基本想法是：这是一个移位寄存器，就LFSR而言，我们现在只有S和R（Shift Registers），所以我们想在想要一个 Feedback（反馈），其基本思想是在每个时钟周期，我们为最后一个触发器（最左边的）产生一个新的输入。我们为最左边的触发器从其他的触发器”计算”一个新的输入。第一种从第一个触发器（最右边的）的输出和中间的触发器的输入异或，得到的结果作为最左边的触发器的输入：

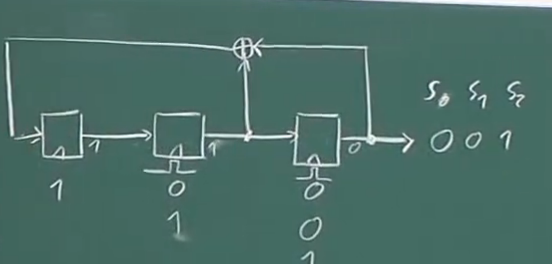
image-20240327214759550

按照上面的规则，根据三个时钟循环，得到下面的数据：

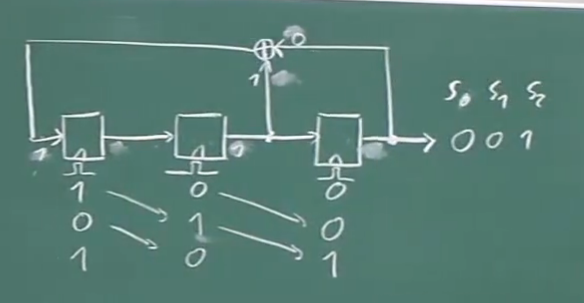
image-20240327215204509

七个时钟循环，结果：

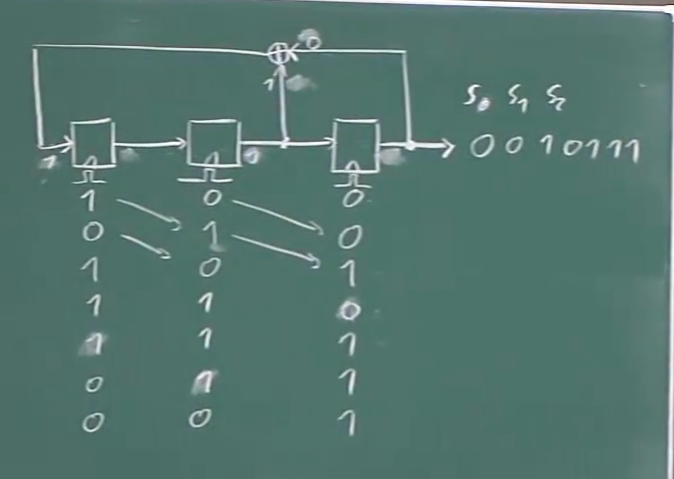
image-20240327215859186

如果我们从三位序列来看（对于三位来说有八个不同的三位值）我们有所有的三位值（少了一个0 0 0），但是当我们计算第八个的时候我们发现，他和第一个是一样的（如下图）我们陷入了一个太近的循环，在第七个时钟周期之后，他回到了第一个，这意味着这是一个周期性的（长度为7的周期），然后开始循环。

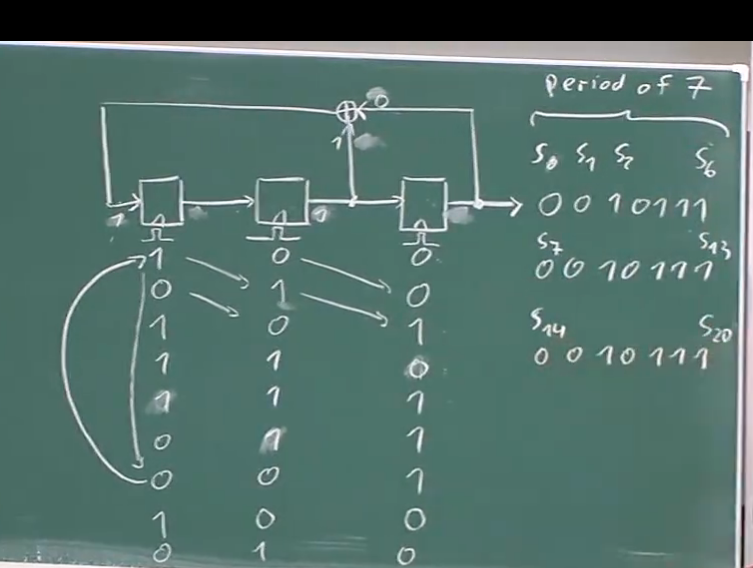
image-20240327222112517

上述所有的东西看起来像是电气工程之类的东西，但是后面是有相关数学理论支撑的

数学公式表达

$$
s_3 \equiv s_1+s_0 \ mod \ 2 \
s_4 \equiv s_2 + s_1 \ mod \ 2 \
s_{i+3} \equiv s_{i+1} + si \ mod \ 2\
$$

常见的LFSRs

我们首先可以操纵的第一件事就是从三个触发器增加到我们想要的数量的触发器。从三个增加数量后，需要注意增加后的触发器中，每一个触发器都有很大的机会和最后的随机数输出异或称为最后一个触发器的输入

每个触发器都变成了一个开关，这些开关引入一个乘数（开关变量），我们将所有的触发器连接在一起（首先先构建成一个移位寄存器）然后再构建反馈网络（每次都是相同的，将输出结果和开关引入的乘数相乘得到X，所有的X来进行异或作为最后一个的输入）

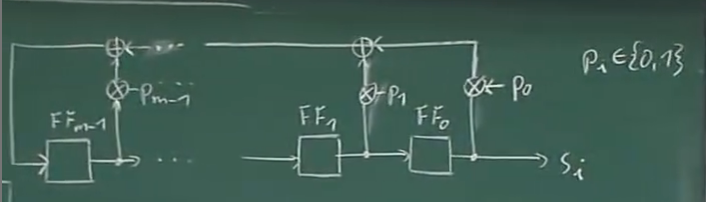
image-20240328084931631

开关乘数的原理：

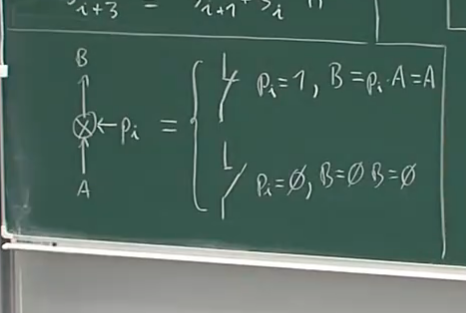
image-20240328084844212

数学公式表达：

$$
S_m \equiv S_{m-1}P_{m-1} + S_{m-2}P_{m-2} + \dots + S_1P_1+S_0P_0 \ mod \ 2 \
S_{m+1} \equiv S_{m}P_{m-1} + S_{m-1}P_{m-2} + \dots + S_2P_1+S_1P_0 \ mod \ 2
$$
Pm是不变的，但是Sm总是递增的，这意味着现在得到了任何输出位的公式

$$ S_{m+i} \equiv \sum^{m-1}_{j=0} S_{i+j} \cdot P_{j} \mod \ 2 ,\ i=0,1,2 $$

P 值是我们决定的（密码设计师决定的），不同的P值最后会得到很大区别的结果

在某段时间后，他会出现一个周期（一段时间后他会开始重复），比如我们上面三个LSR，周期就为7：

image-20240328092626056

定理：m 次LFSR生成的最大周期（或序列长度）为$2^{m}-1$

定理仅适用于某些反馈配置(反馈配置是P的集合($P_{m-1}, \dots ,P_0$)才能产生最大长度序列

Example1：$m=4,P_3=P_2=0，P_1=P_0=1$

(P0是最左边的触发器，P0，P1=1，所以开关闭合，其他的P值为0，不闭合)

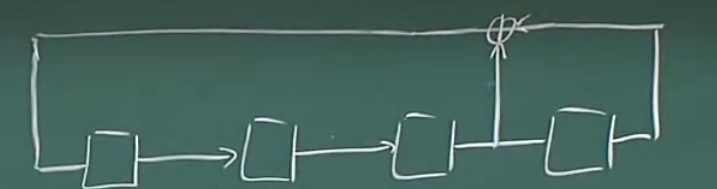
image-20240328200424915

它的最周期是 $2^4-1=15$

Example2：$m=4,P_3=P_2=P_1=P_0=1$

凭直觉来说，这个例子看起来很复杂，但是从密码学上和统计学上，这种情况并不好，无论你的初值是多少，它实际的周期其实是 5

image-20240328200859073

在数学中，不会给出上面这样的图像，一般是采用一种特殊的多项式来表示

符号表示：LFSRs 通常由如下多项式表示
$$
P(x)=x^m+P_{m-1}x^{m-1}+ \dots +P_1x+P_0
$$
所以刚刚上面两个例子中的图，可以化为下面两个不同的多项式：
$$
Ex1:\ X^4+X+1 \
Ex2:\ X^4+X^3+X^2+X+1
$$
当我们看到多项式时，如果告诉我们这是在讨论流密码和LFSRs，那么我们要想到刚刚两个例子的电路图，他们是一回事，是相同的。

如果我们把他们当作多项式，我们可以通过多项式的性质，求出LFSRs何时具有最大长度

如图，下面这些是原始多项式（LFSRs 最大长度的原始多项式）：

image-20240328202240639

通过上图，我们可以看到(0,1,4)这个多项式，对应我们上面的第一个例子，上面第一个例子对应的多项式也是(0,1,4)这个多项式，也就是上面第一个例子，是m=4的情况下，LFSRs最长的情况。

只有具有“原始多项式”的 LFSRs 才能产生最大长度序列

什么是原始多项式？粗略地说，他们和质数有关系

以下回答来自 ChatGPT-4：

“Primitive polynomials” 在密码学中翻译成中文通常是“原始多项式”或“本原多项式”。它们在密码学、编码理论和有限域的理论中扮演着重要的角色。

原始多项式是有限域理论中的一个概念，特别是在构造有限域（也称为Galois域）时非常重要。一个有限域GF(p^n)，其中p是一个素数，n是一个正整数，可以通过取模一个不可约的多项式来构造，如果这个不可约多项式还是一个原始多项式，那么它可以生成该有限域的一个循环乘法群，这在密码学中是非常有用的。

如何计算原始多项式：

  1. 不可约性: 首先，一个原始多项式必须是不可约的，意味着它在其系数所在的有限域上不能被分解成更低次数的多项式的乘积。不可约多项式的判定可以通过多种算法实现，例如Berlekamp算法或Rabin测试。
  2. 原始性测试: 对于一个给定的不可约多项式，要判断它是否是原始的，需要确保它的根是有限域GF(p^n)乘法群的生成元。这可以通过验证多项式的根α的各种幂次能够产生GF(p^n)中的所有非零元素来完成。一个有效的方法是，对于每个小于p^n - 1的正整数d，如果d是p^n - 1的因子，则验证α^d ≠ 1。

与什么有关系：

原始多项式与有限域的构造密切相关。有限域在密码学中有广泛应用，例如在椭圆曲线加密、伪随机数生成、编码理论（如Reed-Solomon编码）以及其他多种加密和数字签名算法中。

简而言之，原始多项式的选择对于有限域的性能和安全性至关重要，它们使得相关的加密系统既高效又安全。

就目前的算力而言，当触发器数量为100时，最长的随机数数量是$2^{100}-1$。这是一个很大的数字，我们无法触发这个LFSRs的循环。但实际上，100个连续触发器是很短的。这意味着，使用移位寄存器，我们拥有一个非常好的构造超长序列的工具（用很少的硬件资源）

上面是一个非常好的伪随机数生成器，但是在密码学上十分糟糕。

针对单个 LFSRs 攻击

Oscar goal：

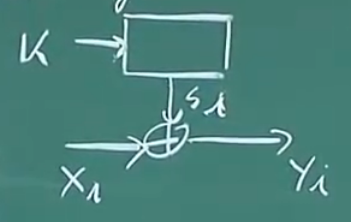
image-20240328213016717

已知条件：

  • 所有的密文
  • m（如果不知道就需要猜，尝试所有的m的情况）
  • $x_0, \dots ,x_{2m-1}$（通过文件头）

开始攻击：

Step1：

$y_i \equiv x_i+s_i \ mod \ 2$

$s_i \equiv y_i+x_i \ mod \ 2$

$i=0,1, \dots,2m-1 $

Step2：

Goal：恢复$S_{2m},S_{2m+1}, \dots$

Q：如果他有m，他缺少的是$P_i$开关的值$P_0=?,P_1=?,\dots,P_{m-1}=?$

我们要回去上面，利用上面的公式

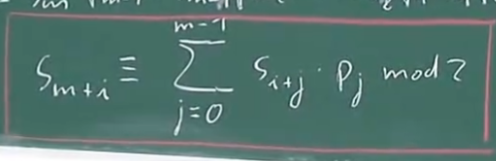
image-20240329103118183

我们想要p的方程，这些都是未知数，我们想最终得到某种公式或算法来解决这个问题。我们首先要写下一个方程，$S_m$是如何计算，我们取和上面完全相同的方程：

$S_m \equiv S_{m-1}P_{m-1}+ \dots + S_0P_0 \ mod \ 2$

我们有了一个方程，这里的未知数有$P_{m-1},\dots,P_0$，好的一面是我们有了一个包含所有未知数的方程，坏的一面是我们只有一个方程，一个m个未知数的线性方程。我们可以利用上面的公式（如下)求出其他的未知数方程：

image-20240328092626056

$S_{m+1} \equiv S_{m-1}P_{m-1}+ \dots +S_0P_0 \ mod \ 2$（未知数不会发生变化）

现在我们又得到了一个方程，虽然我们现在的方程还不够我们破解，但是我们可以继续一遍一遍的重复，直到能够解出未知数，直到：

$S_{2m-1} \equiv S_{2m-2}P_{m-1}+ \dots + S_{m-1}P_0 \ mod \ 2$

m 个未知数的 m 个线性方程组可以通过高斯消去法（或矩阵求逆）轻松解决

以下回答来自ChatGPT-4

在密码学和许多其他领域，高斯消元法是解决线性方程组的一种基础和有效的方法。当你有$m$个未知数和$m$个线性方程时，你可以通过构建一个增广矩阵并使用高斯消元法来求解这个方程组，或者在需要时求出系数矩阵的逆矩阵。这种方法特别适用于需要找到确切解的情况，比如在密码学的某些算法分析中。

步骤 1: 构建增广矩阵

假设你有以下$m$个线性方程组，其中包含$m$个未知数$x_1, x_2, …, x_m$：

$$
\begin{align*}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1m}x_m &= b_1 \newline
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2m}x_m &= b_2 \newline
\vdots \quad & \vdots \newline
a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mm}x_m &= b_m
\end{align*}
$$
你首先构建一个增广矩阵$A|B$，其中$A$是系数矩阵，$B$是常数项列向量：

$$
\begin{align*}
[A|B] = \left[\begin{array}{cccc|c}
a_{11} & a_{12} & \cdots & a_{1m} & b_1 \newline
a_{21} & a_{22} & \cdots & a_{2m} & b_2 \newline
\vdots & \vdots & \ddots & \vdots & \vdots \newline
a_{m1} & a_{m2} & \cdots & a_{mm} & b_m
\end{array}\right]
\end{align*}
$$

步骤 2: 使用高斯消元法

通过一系列的行操作（行交换、行乘以非零常数、行加上另一行的非零常数倍），你可以将增广矩阵转化为行最简形（或阶梯形）。这个过程分为两个主要部分：前向消元和回代。

  • 前向消元：目标是将矩阵转换为上三角形式。你逐行进行，确保每一行的主元（该行最左侧的非零元素）下方的所有元素都是0。
  • 回代：一旦矩阵处于上三角形式，从最后一行开始向上回代，利用当前行的主元解出一个未知数，并将该值代回到上面的所有方程中，逐步解出所有未知数。

步骤 3: 矩阵求逆（可选）

如果目的是求解系数矩阵$A$的逆，这在密码学中用于某些加密算法（如希尔密码）的解密过程，你可以将系数矩阵$A$和单位矩阵$I$放在一起形成增广矩阵$[A|I]$，然后对这个增广矩阵应用高斯消元法。最终，如果$A$是可逆的，你会得到一个形式为$[I|A^{-1}]$的矩阵，其中$A^{-1}$就是$A$的逆矩阵。

注意事项

  • 不是所有矩阵都有逆矩阵。只有当矩阵$A$是方阵且行列式$\det(A) \neq 0$时，$A$才是可逆的。
  • 在密码学应用中，特别是在模运算下解线性方程组时，所有计算（包括求逆）都需要在给定模数下进行。

通过这种方法，高斯消元法为密码学提供了一种在理论和实践中都非常重要的工具，用于解决线性方程组，以及在某些情况下，帮助破解或分析加密算法。

如果攻击者（至少）知道 LFSR 的 2m 个输出值，他可以恢复整个 LFSR 配置

当攻击者知道了$P_i$后，可以完全指定LFSR，即它可以自己构建LFSR，这里第三步是生成是生成所有

Step3：

  • 使用$P_{m-1},\dots,P_0$构建LFSR
  • 计算$S_0,\dots\ ,S_{2m-}, S_{2m},S_{2m+1}, \dots$以此类推，计算整个输出
  • 解码：$X_i\equiv Y_i+Si \ mod \ 2 \ \ \ \ i=0,1,2,\dots$

有很长的序列长度，虽然从数据上看起来它们很好，很容易构建，但是在数学上有一些奇怪的描述，他们实际上并不安全。

但是可以用他们好几个，一起像积木一样堆叠起来来生成安全的密码