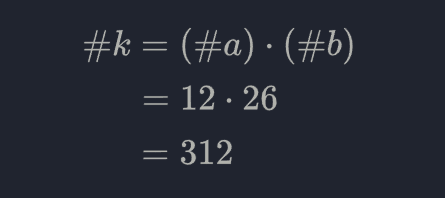根据德国 Christof Paar 的密码学基础教程学习了一些入门的密码学知识，本文对应其第二节内容，主要关于模运算（Modular Arithmetic），等价类（Equivalence Classes），环（Ring），凯撒密码（Caesar cipher），仿射密码（affine cipher）

古典密码

Modular Arithmetic 模运算

定义：

令 $a,r,m\in Z,$ 并且 $m>0$ 我们记作 $a\equiv r\ mod \ m$如果中位数$(a-r)$最高的$m|(a-r)$（m除以 (a-r)）

$m|(a-r)$读作 m除以（a-r)

r ：remainder 余

m：modulus 模数

举例：
$$
a = 13, m=9\quad r=?
$$

$$
13 \equiv 4 \ mod \ 9
$$

$$
a -r=(13-4)=9
$$

computation of the remainder 余数的计算

通常给出 $ a,m \in Z，a = q* m+r$

(q：quotient 商)

example：
$$
a=42,m=9
$$

$$
42=4*9+6 \Rightarrow r=6
$$

通过定义对刚刚的计算进行检测：
$$
(42-6) = 36, 9\ |\ 36 满足
$$
注意：余数不唯一

Equivalence Classes 等价类

example：
$$
a=12,m=5
$$

$$
12 \equiv2 \ mod \ 5 \ check \ 5\ | \ (12-2)
$$

$$
12 \equiv 7 \ mod \ 5 \ check \ 5 \ | \ (12-7)
$$

$$
12 \equiv -3 \ mod \ 5 \ check \ 5 \ | \ (12 -(-3))
$$

定义：该结合{...,-8,-3,2,7,12,15,...}形成一个“等价类”，这个集合中的所有元素在模5下具有相同的行为或特征。

接下来查看所有以 5 为模的等值类：

{...,-15,-10,-5,0,5,10,15,...} —— A

{...,-14,-9,-4,1,6,11,16,...} —— B

{...,-13,-8,-3,2,7,12,17,...} —— C

{...,-12,-7,-2,3,8,13,18,...} —— D

{...,-11,-6,-1,4,9,14,19,...} —— E

计算$1316-8=208 -8=200 \equiv 0 \ mod \ 5$ 。我们可以将这个计算看为：
$$
D * B -D
$$
进一步代数：$\ 31-3=3-3 \equiv 0 \ mod \ 5$

这里就利用了刚刚等价类的定义：

Important application 重要应用

大多数非对称密码加密是基于模运算的。

example：在公钥密码学中有一个非常经典的情况：在建立安全连接时（如 https）有很大的数据量，其中大多数用到了指数运算，对于特大的数据，直接通过计算机计算需要消耗大量的时间进行计算，所以有时候使用一些别的计算方法来减少我们的计算时间。
$$
3^8 \ mod \ 7 \equiv \ ?
$$
1） $3^8=6567 \equiv \ 2 \ mod \ 7$

2) $3^{8}=3^{4}\cdot3^{4} =81 \cdot 81 \equiv \ 4\cdot4=16 \equiv 2 \ mod \ 7$

上面的第一种方法，就是直接计算，然后进行模运算，能够看到，需要进行大量的计算。

第二种方法使用了我们刚刚的等价类的性质，我们通过指数运算的性质，将其拆解为：$ 3^8=3^4*3^4$ 这样我们得到了$81 *81$ 接着：
$$
81\cdot81=(11\cdot7+4)\cdot81=4\cdot4=16 \equiv 2\ mod \ 7
$$
也可以继续抽象：
$$
3^{8}=3^{2}\cdot3^{2}\cdot3^{2}\cdot3^{2}=9\cdot9\cdot9\cdot9=(1\cdot7+2)\cdot9\cdot9\cdot9= 2\cdot2\cdot2\cdot2=16 \equiv 2 \ mod \ 7
$$

在数学上，选择等价类中的某个数字都是成立的，但是我们通常选择最小的，正的等价类来进行运算，比如：

Rings: An algebraic view on modular arithmetic 环：模运算的代数观点

定义：“整数环”$Z_m$由

集合 $Z_m = {0,1,2, \ldots ,m-1 } $
两个运算符$+ \ *$组成。使得对于所有 $a, b, c,d \in Z_m$

i) $a+b \equiv c \ mod \ m$

ii) $a*b \equiv d \ mod \ m$

在后续的还会遇到很多的环，比如：多项式形成环矩阵环

性质：

我们可以对任意两个数字进行加法和乘法，结果总是在环中。环被称为闭合环
加法和乘法都存在结合率，e.g.$a+(b+c)=(a+b)+c \ 且 a ·(b · c) = (a · b)· c , all \ a,b,c \in Z_m$
对于加法，存在中性元素 0，即，对于每个元素 $a \in Z_m$，它都满足 $a+0 \equiv a \ mod \ m$。
对于环中的任意元素 a，总存在负元素 −a，使得$a+(−a) ≡ 0 \ mod \ m$，即加法逆元总是存在。
对于乘法，存在中性元素 1，即，对于每个元素 $a ∈ Z_m$，它都满足 $a×1 \equiv a\ mod \ m$。
乘法逆元仅适用于某些元素，但不适用于所有元素。设 a ∈ Z，逆元 a^−1^ 定义为
$$
a·a^{-1} \equiv 1 \ mod\ m
$$
如果 a 存在逆元，我们可以除以该元素，因为 $b/a == b · a
−1 \ mod \ m$。
如果 a 存在逆元，我们可以除以该元素，因为 b/a == b · a −1 mod m。找到逆矩阵需要付出一些努力（通常采用欧几里得算法，这在第 6.3 节中进行了介绍）。

然而，有一个简单的方法可以告诉你给定元素 a 的逆是否存在：元素 a ∈ Z 具有乘法逆元 a^−1^ 当且仅当 gcd(a,m) = 1，其中 gcd 是最大公约数，即整除的最大整数两个数字 a 和 m。两个数字的 gcd 为 1 的事实非常重要在数论中很重要，并且有一个特殊的名称：if gcd(a,m) = 1, 那么 a 和 m 被称为互素或互质。

example： multiplicative inverses 乘法逆元

$$
m=9,Z_9= {0,1,2,3,4,5,\ldots} \ a=2\ a^{-1}=?
$$
这里我们可以通过看看出，在 m = 9 的情况下，2 的逆元是 5：
$$
2 * 2^{-1} \equiv 1 \ mod \ 9
\ 2*5 \equiv 1 \ mod\ 9
$$
但是 6 的逆元，我们没办法向刚刚的方法直接看出来。我们在这里进行一步验证：gcd(6,9)=3 （gcd(a,b)表示 a，b的最大公约数）。但是看我们刚刚的例子：gcd(2,9)=1。所以：

如果两个数的最大公约数不等于1(gcd(a,b)!=1)那么则不存在逆元

shift (or caesar) cipher 移位（凯撒）密码

想法：在字母表中移动字母

example： k = 3 那么存在字母表对应关系：

A -> d
B -> e
...
W -> z
X -> a
Y -> b
Z -> c

最后三个就是一个环绕回到了前三个没用的字母。

实现上面的过程是通过一个非常漂亮的方式modulo 26自动完成的

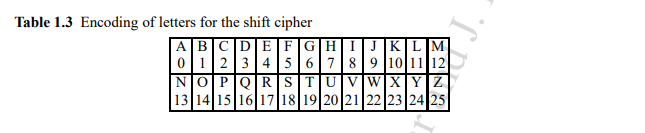
上面的是通过手算，手写密码表来实现的，我们可以使用数学方法来实现加密，解密的过程：

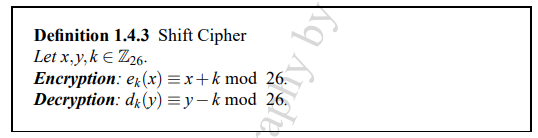
攻击方法有两种：

频率分析
密钥搜索（暴力破解，蛮力攻击）

affine cipher 仿射密码

example：key = (a, b) 那么：
$$
enc: \ y \equiv a\cdot x+b \ mod\ 26\
y-b \equiv a \cdot x\ mod \ 26 \
a^{-1} \cdot(y-b) \equiv x \ mod \ 26 \
dec: \ x \equiv a^{-1}(y-b) \ mod\ 26
$$

问题在于#k = ?（#代表空间，那么#k 代表密钥空间）即：密钥有多少个键，首先我们要知道系统中有多少个 a 和多少个 b 从简单的开始：

#b=26 使用 a 的条件是gcd(a, 26)=1，满足条件的 a 有$(1, 3, 5, 7, 9 ,11,\ldots \Rightarrow \# a=12)$

那么：

Q1ngying

密码-1：模运算，凯撒密码，仿射密码